UID159057
её–еӯҗ
зІҫиҸҜ
дё»йЎҢ
з©ҚеҲҶ2380
зҸҫйҮ‘
з©ҚжҘөжҖ§
еЁҒжңӣ
йҒ•иҰҸ
зҶұеҝғ
жҺЁе»Јж¬Ўж•ё
й–ұи®Җж¬Ҡйҷҗ10
иЁ»еҶҠжҷӮй–“2009-5-26
еңЁз·ҡжҷӮй–“ е°ҸжҷӮ
жңҖеҫҢзҷ»йҢ„1970-1-1
TAзҡ„жҜҸж—Ҙеҝғжғ… | й–Ӣеҝғ
2018-12-14 06:21 PM |
|---|
з°ҪеҲ°еӨ©ж•ё: 123 еӨ© йҖЈзәҢз°ҪеҲ°: 2 еӨ© [LV.7]еёёдҪҸеұ…ж°‘III
|
жңүдёҖйғЁи»ҠеӯҗпјҢе…Ёйӣ»и…ҰиЈқзҪ®пјҢжңүйҮҢзЁӢе„Җ (Odometer) иҲҮйҖҹзҺҮе„Җ (speedometer)пјҢиҖҢдё”йғҪжҳҜз”ЁеқҗжЁҷең–еҪўдҫҶиЎЁйҒ”гҖӮеҒҮиЁӯйҖҹзҺҮе„Җж•…йҡңпјҢеҸӘеү©йҮҢзЁӢе„ҖгҖӮдәӨйҖҡиӯҰеҜҹж””дёӢйҖҷйғЁи»ҠеӯҗпјҢиӘӘжҳҜи¶…йҖҹпјҢ駕й§ӣиҫҜзЁұпјҡжҲ‘жІ’жңүи¶…йҖҹпјҢиӢҘжңүзҡ„и©ұпјҢи«ӢиӯҰеҜҹе…Ҳз”ҹжӢҝеҮәиЁјж“ҡгҖӮ
иӯҰеҜҹиӘӘпјҡз”ұдҪ зҡ„йҮҢзЁӢе„Җзҡ„ең–еҪўзҹҘйҒ“ 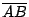 зҡ„ж–ңзҺҮеӨ§ж–јйҷҗйҖҹпјҢдёҰдё” t0 жҷӮеҲ»зҡ„еҲҮз·ҡж–ңзҺҮпјҲеҚіи»Ҡеӯҗзҡ„йҖҹзҺҮпјүзӯүж–ј зҡ„ж–ңзҺҮеӨ§ж–јйҷҗйҖҹпјҢдёҰдё” t0 жҷӮеҲ»зҡ„еҲҮз·ҡж–ңзҺҮпјҲеҚіи»Ҡеӯҗзҡ„йҖҹзҺҮпјүзӯүж–ј 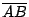 зҡ„ж–ңзҺҮпјҢж•…дҪ еңЁ t0 жҷӮеҲ»и¶…йҖҹгҖӮйҖҷдҪҚиӯҰеҜҹжҮӮеҫ—еҫ®з©ҚеҲҶпјҢдёҠиҝ°зҡ„и«–иЁјз”ЁеҲ°дәҶе№іеқҮеҖје®ҡзҗҶпјҡ е№іеқҮеҖје®ҡзҗҶ: еҒҮиЁӯ 1. f еңЁй–үеҚҖй–“ [a,b] дёҠйҖЈзәҢпјҢ 2. f еңЁй–ӢеҚҖй–“ (a,b) дёҠеҸҜеҫ®еҲҶгҖӮ еүҮеӯҳеңЁ зҡ„ж–ңзҺҮпјҢж•…дҪ еңЁ t0 жҷӮеҲ»и¶…йҖҹгҖӮйҖҷдҪҚиӯҰеҜҹжҮӮеҫ—еҫ®з©ҚеҲҶпјҢдёҠиҝ°зҡ„и«–иЁјз”ЁеҲ°дәҶе№іеқҮеҖје®ҡзҗҶпјҡ е№іеқҮеҖје®ҡзҗҶ: еҒҮиЁӯ 1. f еңЁй–үеҚҖй–“ [a,b] дёҠйҖЈзәҢпјҢ 2. f еңЁй–ӢеҚҖй–“ (a,b) дёҠеҸҜеҫ®еҲҶгҖӮ еүҮеӯҳеңЁ 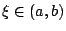 дҪҝеҫ— дҪҝеҫ—
е®ғзҡ„зү№дҫӢжҳҜ Rolle е®ҡзҗҶпјҢдҪҶжҳҜжҲ‘еҖ‘еҸҜд»ҘеҲ©з”Ё Rolle е®ҡзҗҶдҫҶиЁјжҳҺе№іеқҮеҖје®ҡзҗҶпјҢеӣ жӯӨпјҢе…©иҖ…зӯүеғ№гҖӮ Rolle е®ҡзҗҶ: еҒҮиЁӯ 1. f еңЁй–үеҚҖй–“ [a,b] дёҠйҖЈзәҢпјҢ 2. f еңЁй–ӢеҚҖй–“ (a,b) дёҠеҸҜеҫ®еҲҶпјҢ 3. f(a)=0=f(b)гҖӮ еүҮеӯҳеңЁ 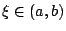 пјҢдҪҝеҫ— пјҢдҪҝеҫ— 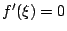
當еҲқ Rolle и§ҖеҜҹеҲ°пјҢиӢҘеӨҡй …ејҸж–№зЁӢејҸ f(x)=0 жңү a, b е…©ж №пјҢеҚі f(a)=0=f(b)пјҢеүҮж–№зЁӢејҸ f'(x)=0 еңЁ (a,b) д№ӢдёӯиҮіе°‘еӯҳеңЁжңүдёҖж № ОҫпјҢеҚі 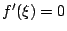 гҖӮйҖҷжҳҜ Rolle е®ҡзҗҶзҡ„иө·жәҗгҖӮ е№іеқҮеҖје®ҡзҗҶжңүдёүеҖӢж–№еҗ‘д№ӢжҺЁе»Јпјҡ жі°еӢ’е®ҡзҗҶ: иЁӯ f еңЁ гҖӮйҖҷжҳҜ Rolle е®ҡзҗҶзҡ„иө·жәҗгҖӮ е№іеқҮеҖје®ҡзҗҶжңүдёүеҖӢж–№еҗ‘д№ӢжҺЁе»Јпјҡ жі°еӢ’е®ҡзҗҶ: иЁӯ f еңЁ 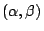 дёҠжҳҜзӣҙеҲ° n+1 йҡҺйҖЈзәҢеҸҜеҫ®еҲҶзҡ„еҮҪж•ёпјҢдё” дёҠжҳҜзӣҙеҲ° n+1 йҡҺйҖЈзәҢеҸҜеҫ®еҲҶзҡ„еҮҪж•ёпјҢдё” 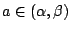 пјҢеүҮе°Қд»»дҪ• пјҢеүҮе°Қд»»дҪ• 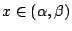 пјҢf(x) еҸҜд»Ҙеұ•жҲҗдёӢејҸ пјҢf(x) еҸҜд»Ҙеұ•жҲҗдёӢејҸ
е…¶дёӯ Оҫ зӮәд»Ӣж–ј x иҲҮ a д№Ӣй–“зҡ„дёҖеҖӢж•ёгҖӮ иЁ»пјҡжі°еӢ’е®ҡзҗҶжҳҜе°ҚдёҖйЎһзӣёз•¶еҘҪзҡ„еҮҪж•ёдҪңеү–жһҗпјҢжүҖеҫ—еҲ°зҡ„еҮҪж•ёзҡ„зөҗж§Ӣе®ҡзҗҶгҖӮ Cauchy зҡ„е№іеқҮеҖје®ҡзҗҶ: еҒҮиЁӯ (i) f иҲҮ g еңЁ [a,b] дёҠйҖЈзәҢпјҢ (ii) f иҲҮ g еңЁ (a,b) дёҠеҸҜеҫ®еҲҶпјҢ (iii) 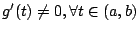 гҖӮ еүҮеӯҳеңЁ гҖӮ еүҮеӯҳеңЁ 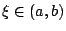 дҪҝеҫ— дҪҝеҫ—
иЁ»пјҡCauchy зҡ„е№іеқҮеҖје®ҡзҗҶжҳҜ L'HospitalиҰҸеүҮ зҡ„зҗҶи«–еҹәзӨҺгҖӮ жҺЁе»Јзҡ„е№іеқҮеҖје®ҡзҗҶ: иЁӯ f, g, h еңЁ [a,b] дёҠйҖЈзәҢпјҢеңЁ (a,b) дёҠеҸҜеҫ®еҲҶпјҢеүҮеӯҳеңЁ 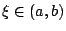 дҪҝеҫ—иЎҢеҲ—ејҸ дҪҝеҫ—иЎҢеҲ—ејҸ
иЁ»пјҡ (i)當 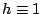 жҷӮпјҢйҖҷеҖӢе®ҡзҗҶе°ұеҢ–зҙ„зӮә Cauchy зҡ„е№іеқҮеҖје®ҡзҗҶгҖӮ (ii)當 жҷӮпјҢйҖҷеҖӢе®ҡзҗҶе°ұеҢ–зҙ„зӮә Cauchy зҡ„е№іеқҮеҖје®ҡзҗҶгҖӮ (ii)當 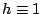 дё” g(x)=x жҷӮпјҢйҖҷеҖӢе®ҡзҗҶе°ұеҢ–зҙ„зӮәе№іеқҮеҖје®ҡзҗҶгҖӮ жүҖи¬Ӯ Newton-Leibniz е…¬ејҸжҳҜжҢҮпјҡ еҒҮиЁӯ F еңЁ [a,b] дёҠдёҖйҡҺйҖЈзәҢеҸҜеҫ®еҲҶпјҢеүҮ дё” g(x)=x жҷӮпјҢйҖҷеҖӢе®ҡзҗҶе°ұеҢ–зҙ„зӮәе№іеқҮеҖје®ҡзҗҶгҖӮ жүҖи¬Ӯ Newton-Leibniz е…¬ејҸжҳҜжҢҮпјҡ еҒҮиЁӯ F еңЁ [a,b] дёҠдёҖйҡҺйҖЈзәҢеҸҜеҫ®еҲҶпјҢеүҮ
жҲ‘еҖ‘еҸҜд»ҘиЁјжҳҺе№іеқҮеҖје®ҡзҗҶиҲҮ Newton-Leibniz е…¬ејҸзӯүеғ№гҖӮ иЁјжҳҺ: е№іеқҮеҖје®ҡзҗҶ 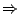 Newton-Leibniz е…¬ејҸпјҢиЁӯ Newton-Leibniz е…¬ејҸпјҢиЁӯ
жҳҜ [a,b] зҡ„дёҖеҖӢеҲҶеүІгҖӮз”ұе№іеқҮеҖје®ҡзҗҶзҹҘпјҢй»Һжӣје’Ң
еҸ–жҘөйҷҗе°ұеҫ—еҲ° Newton-Leibniz е…¬ејҸгҖӮ еҸҚйҒҺдҫҶпјҢNewton-Leibniz е…¬ејҸ 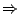 е№іеқҮеҖје®ҡзҗҶпјҡз”ұз©ҚеҲҶзҡ„е№іеқҮеҖје®ҡзҗҶзҹҘпјҢеӯҳеңЁ е№іеқҮеҖје®ҡзҗҶпјҡз”ұз©ҚеҲҶзҡ„е№іеқҮеҖје®ҡзҗҶзҹҘпјҢеӯҳеңЁ 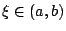 дҪҝеҫ— дҪҝеҫ—
еҶҚй…ҚеҗҲ Newton-Leibniz е…¬ејҸпјҢз«Ӣеҫ—е№іеқҮеҖје®ҡзҗҶ
з”ұдёҠиҝ°зңӢдҫҶпјҢе№іеқҮеҖје®ҡзҗҶеңЁеҫ®з©ҚеҲҶдёӯдҪ”жңүж ёеҝғзҡ„ең°дҪҚгҖӮ е№іеқҮеҖје®ҡзҗҶйӮ„жңүдёҖеұӨж„Ҹзҫ©пјҡе°Үж¶үеҸҠз„ЎзӘ®жӯҘй©ҹзҡ„жҘөйҷҗ
з”Ёжңүйҷҗзҡ„зүӣй “е•Ҷ
дҫҶеҸ–д»ЈпјҢе…·жңүд»Ҙз°ЎеҫЎз№Ғзҡ„ж„Ҹе‘іпјҢдҪҶд»ҳеҮәдёҖй»һд»Јеғ№пјҡжҲ‘еҖ‘е°Қ Оҫ зҡ„дҪҚзҪ®дёҚеӨӘжё…жҘҡгҖӮ |
|