UID159057
帖子
精華
主題
積分2380
現金
積極性
威望
違規
熱心
推廣次數
閱讀權限10
註冊時間2009-5-26
在線時間 小時
最後登錄1970-1-1
TA的每日心情 | 開心
2018-12-14 06:21 PM |
|---|
簽到天數: 123 天 連續簽到: 2 天 [LV.7]常住居民III
|
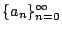 可看成是定義在非負整數集上的函數,其於整數 可看成是定義在非負整數集上的函數,其於整數 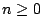 之值就是 an。差分算子 Δ(difference operator)是一在這些函數組成的集合上之變換,其定義為 之值就是 an。差分算子 Δ(difference operator)是一在這些函數組成的集合上之變換,其定義為
高階差分算子 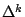 (k=2,3,…)是定義為 (k=2,3,…)是定義為
我們並定義 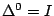 ,其中 I 是恆等算子,即 Ian=an (n=0,1,2,…)。與差分算子有密切關係的是位移算子 E (Translation operator),其定義為 ,其中 I 是恆等算子,即 Ian=an (n=0,1,2,…)。與差分算子有密切關係的是位移算子 E (Translation operator),其定義為
Ean=an+1
高階位移算子 Ek (k=2,3,…) 是定義為
Ekan=E(Ek-1an)=an+k
我們並定義 E0=I,顯見有 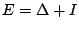 。任何方程含有差分算子或與其等價之位移算子的稱為差分方程 (difference equation)。一個 k階常係數線性差分方程 (或回歸方程)有一般形式 。任何方程含有差分算子或與其等價之位移算子的稱為差分方程 (difference equation)。一個 k階常係數線性差分方程 (或回歸方程)有一般形式
其中 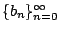 是一給定數列,C0, C1, …, Ck 是給定之常數。如果有 k 個相連的值為給出,稱為邊界條件,則方程(6)有唯一的解。與 (6)對應之齊次差分方程是 是一給定數列,C0, C1, …, Ck 是給定之常數。如果有 k 個相連的值為給出,稱為邊界條件,則方程(6)有唯一的解。與 (6)對應之齊次差分方程是
前述之方程 (1)與 (4)均是一階非齊次差分方程;方程 (5)是二階齊次差分方程。利用位移算子,方程 (6)與 (7)又可記為
及
方程 (9)之解稱為齊次解;任意滿足方程 (8) 之解稱特別解。讀者已可觀察到 k階常係數線性差分方程與微積分中的 k 階常係數線性微分方程之間相似性;實際上它們之間有許多相平行的性質。例如所有齊次解形成的集合是一向量空間;方程(8)之解必為一個齊次解及某個特別解之和。這些性質的證明與微分方程中相應性質的證明相似,我們不在此詳細說明。有關差分方程一般性質請參閱參考資料[1]。 下面我們討論 k階齊次常係數線性差分方程 (9)之求解步驟。在 (9)中令 an=rn,我們有
我們不考慮 r=0的情況,故又有
方程 (10)是一次代數方程式,稱為與 (9)對應之特徵方程式;它有 k個根,稱為方程 (9)之特徵根。如果 (10)有 k個不同的根 r1, r2, …, rk,則任一方程 (9)之解有形式
其中 A1, A2, …, Ak 是未定係數,由所給出的邊界條件所決定。如果一特徵根 r是 (10)之 m 重根,則與之對應的齊次解是
如果方程 (10)有一對共軛複根 p+qi 及 p-qi,則與之對應之齊次解又可寫成
其中 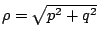 , , 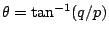 ,B1=A1+A2 及 B2=i(A1-A2)。下面我們在用例題來說明齊次差分方程之求解步驟。 [例4] ,B1=A1+A2 及 B2=i(A1-A2)。下面我們在用例題來說明齊次差分方程之求解步驟。 [例4]
解例3中的齊次差分方程 (5):
方程 (11)之特徵方程是
r2-r-1=0
它有兩個不同的特徵根 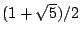 與 與 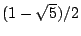 ,故其齊次解有形式 ,故其齊次解有形式
為了決定未定係數 A1 與 A2,我們將(11)中之邊界條件代入(12)得
解聯立方程 (13)得
因此方程 (11)之解是
[例5] 計算 n 階行列式
設 (14)中之 n階行列式之值為 an,由第一列將 (14)展開得差分方程
它的特徵方程是 r2-r+1=0,故有兩個共軛複根
得方程 (15)之齊次解有形式
將 (15)中之邊界條件代入 (16)有
從而得未定係數 B1=1, 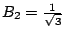 。方程(15)之解是 。方程(15)之解是
由方程 (15)可見由 n=1起 an之值的首幾項是
最後我們介紹一種非齊次差分方程 (8)的求解步驟。由上面討論知只需求出方程 (8)的某個特別解。我們所用的是一種經驗法,是由方程 (8)之右邊 bn之形式來判斷特別解可能有的形式,然後再決定其中未定係數。下表列出幾種常遇到的 bn形式
其中表之右列中 B,B1,B2,…,Bp 為未定係數。這種解法也是求常微分方程之非齊次解時常用方法之一,讀者應對這兩種情況之異同作一比較。 [例6] 問在由 0,1,2,3 所組成的 n 位數中有多少含有偶數個零? 設 an 是由 0,1,2,3 所組成的 n 位數中含偶數個 0 的個數,則在這些數中,最後一位數或者不為零,這樣的數有 3an-1 個;或者最後一位數為零,則它前面 n-1位中必有奇數個零,這樣的數一共有 4n-1-an-1 個,故得 an=3an-1+4n-1-an-1。顯然有 a1=3,故所求的差分方程可寫成
方程 (18)之特徵方程式 r-2=0,它有唯一的特徵根 r=2,故得方程(18)之齊次解有形式
an=A2n
其中 A 是未定係數。為了求方程的特別解,由表(17)得它有形式 an=B4n,其中 B為未定係數。代入方程(18)得
B4n+1-2B4n=4n
從而 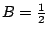 。因此方程(18)之任一解均有形式 。因此方程(18)之任一解均有形式
將(18)中邊界條件代入(19)得 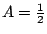 ,因此方程(18)之解為 ,因此方程(18)之解為
用試驗解法求特別解也有失效的情況,那時我們必需作必要的修正。最後我們舉下例來說明此點。 [例7] 解差分方程
方程 (20)的特徵方程是 r-1=0,故它有唯一的特徵根 r=1。因此方程(20)的齊次解是 an=A(1)n=A,其中 A 是未定係數。根據表(17)方程(20)的特別解有形式
但齊次解與特別解中均有一項是常數,將 (21)代入 (20)將無法決定未定係數 B1。這時我們可以將特別解乘一最低次數之 n 的整數冪,使得齊次解與特別解中的這種相似項消失。因此我們可令方程(20)之特別解有形式 an=B1n+B2n2 並代入(20)得
B1(n+1)+B2(n+1)2-B1n-B2n2 = 2n
比較兩邊係數得 B1=-1, B2=1。方程(20)之任一解均有形式
將(20)中之邊界條件代入(21)得 A=2,因此方程(20)之解為
an=n2-n+2 |
|