UID159057
её–еӯҗ
зІҫиҸҜ
дё»йЎҢ
з©ҚеҲҶ2380
зҸҫйҮ‘
з©ҚжҘөжҖ§
еЁҒжңӣ
йҒ•иҰҸ
зҶұеҝғ
жҺЁе»Јж¬Ўж•ё
й–ұи®Җж¬Ҡйҷҗ10
иЁ»еҶҠжҷӮй–“2009-5-26
еңЁз·ҡжҷӮй–“ е°ҸжҷӮ
жңҖеҫҢзҷ»йҢ„1970-1-1
TAзҡ„жҜҸж—Ҙеҝғжғ… | й–Ӣеҝғ
2018-12-14 06:21 PM |
|---|
з°ҪеҲ°еӨ©ж•ё: 123 еӨ© йҖЈзәҢз°ҪеҲ°: 2 еӨ© [LV.7]еёёдҪҸеұ…ж°‘III
|
дҫӢ4пјҡ гҖҢзү©дёҚзҹҘе…¶ж•ёпјҢдёүдёүж•ёд№Ӣеү©дәҢпјҢдә”дә”ж•ёд№Ӣеү©дёүпјҢдёғдёғж•ёд№Ӣеү©дәҢгҖҚеҸҜз”ЁеҗҢйӨҳејҸиЎЁзӨәеҰӮдёӢгҖӮ
гҖҢйҹ“дҝЎй»һе…өе•ҸйЎҢгҖҚе°ұжҳҜжұӮдёҖзө„еҗҢйӨҳејҸзҡ„е…¬и§ЈгҖӮгҖҢ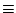 гҖҚиҲҮзӯүејҸгҖҢпјқгҖҚжңүеҗҢжЁЈзҡ„йҒӢз®—жі•еүҮпјҢйӮЈе°ұжҳҜиӘӘпјҡ е®ҡзҗҶ1пјҡе·ІзҹҘ гҖҚиҲҮзӯүејҸгҖҢпјқгҖҚжңүеҗҢжЁЈзҡ„йҒӢз®—жі•еүҮпјҢйӮЈе°ұжҳҜиӘӘпјҡ е®ҡзҗҶ1пјҡе·ІзҹҘ 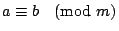 пјҢ пјҢ 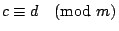 пјҢйӮЈйәјпјҢ пјҢйӮЈйәјпјҢ 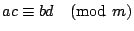 пјҢ пјҢ 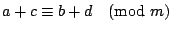 пјҢ пјҢ 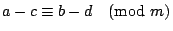 пјҢ пјҢ 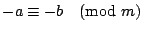 пјҢ пјҢ 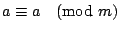 гҖӮ гҖӮ
иӯүжҳҺпјҡжҲ‘еҖ‘е…Ҳиӯү 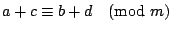 пјҢи®ҖиҖ…еҸҜд»Ҙд»ҝз…§жҲ‘еҖ‘зҡ„иӯүжі•пјҢеҺ»иӯүжҳҺе…¶йӨҳе…¬ејҸгҖӮ ж №ж“ҡгҖҢ пјҢи®ҖиҖ…еҸҜд»Ҙд»ҝз…§жҲ‘еҖ‘зҡ„иӯүжі•пјҢеҺ»иӯүжҳҺе…¶йӨҳе…¬ејҸгҖӮ ж №ж“ҡгҖҢ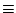 гҖҚзҡ„е®ҡзҫ©пјҢжҲ‘еҖ‘зҹҘйҒ“ a-b = smпјҢc-d = tm жүҖд»Ҙ гҖҚзҡ„е®ҡзҫ©пјҢжҲ‘еҖ‘зҹҘйҒ“ a-b = smпјҢc-d = tm жүҖд»Ҙ
(a+c) - (b+d) = (a-b)+(c-d) = sm+tm = (s+t)m
йӮЈе°ұжҳҜиӘӘпјҢ 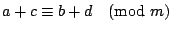 иӯүе®ҢгҖӮ еңЁжҺЁжј”еӯ«еӯҗе®ҡзҗҶпјҲдёӯеңӢеү©йӨҳе®ҡзҗҶпјүзҡ„йҒҺзЁӢдёӯпјҢжҲ‘еҖ‘й ҲиҰҒдёҖеҖӢжҮүз”Ёе…©ж•ёдә’иіӘпјҲе…©ж•ёзҡ„жңҖеӨ§е…¬зҙ„ж•ёжҳҜ1пјүзҡ„е®ҡзҗҶпјҢйӮЈе°ұжҳҜпјҡ е®ҡзҗҶ2пјҡе·ІзҹҘ m,n йҒ©еҗҲдёӢејҸпјҢ am+bn=1пјҢйӮЈйәј m,n дә’иіӘпјҢеҸҚйҒҺдҫҶиӘӘпјҢеҰӮжһң m,n дә’иіӘпјҢжҲ‘еҖ‘еҸҜд»ҘжүҫеҲ° a,bпјҢдҪҝеҫ— иӯүе®ҢгҖӮ еңЁжҺЁжј”еӯ«еӯҗе®ҡзҗҶпјҲдёӯеңӢеү©йӨҳе®ҡзҗҶпјүзҡ„йҒҺзЁӢдёӯпјҢжҲ‘еҖ‘й ҲиҰҒдёҖеҖӢжҮүз”Ёе…©ж•ёдә’иіӘпјҲе…©ж•ёзҡ„жңҖеӨ§е…¬зҙ„ж•ёжҳҜ1пјүзҡ„е®ҡзҗҶпјҢйӮЈе°ұжҳҜпјҡ е®ҡзҗҶ2пјҡе·ІзҹҘ m,n йҒ©еҗҲдёӢејҸпјҢ am+bn=1пјҢйӮЈйәј m,n дә’иіӘпјҢеҸҚйҒҺдҫҶиӘӘпјҢеҰӮжһң m,n дә’иіӘпјҢжҲ‘еҖ‘еҸҜд»ҘжүҫеҲ° a,bпјҢдҪҝеҫ—
am+bn=1
иӯүжҳҺпјҡеӣ зӮә m,n зҡ„жңҖеӨ§е…¬зҙ„ж•ёеҸҜд»Ҙж•ҙйҷӨ am+bnпјҢиҖҢ am+bn=1пјҢжүҖд»Ҙ m,n зҡ„жңҖеӨ§е…¬зҙ„ж•ёжҳҜ1пјҢжҸӣеҸҘи©ұпјҢ m,n дә’иіӘгҖӮеҸҚйҒҺдҫҶиӘӘпјҢеҰӮжһңе·ұзҹҘ m,n дә’иіӘпјҢи®ҖиҖ…еҸҜд»ҘжҮүз”ЁијҫиҪүзӣёйҷӨжі•пјҢжұӮеҫ— a,b дҪҝеҫ— am+bn=1пјҢиӯүе®ҢгҖӮ жҮүз”Ёе®ҡзҗҶ2пјҢжҲ‘еҖ‘еҸҜд»Ҙи§Јзӯ”жјӮжҜҚж•ёеёғеҢ№зҡ„е•ҸйЎҢдәҶпјҢйӮЈе°ұжҳҜдёӢйқўзҡ„е®ҡзҗҶ3: е®ҡзҗҶ3пјҡе·ұзҹҘ m,n дә’иіӘпјҢйӮЈйәјдёӢеҲ—дёҖзө„еҗҢйӨҳејҸпјҡ
жңүе…¬и§ЈгҖӮ
иӯүжҳҺпјҡж №ж“ҡе®ҡзҗҶ2пјҢжҲ‘еҖ‘еҸҜд»ҘжүҫеҲ° a,b дҪҝеҫ— am+bn=1пјҢжүҖд»Ҙ bn=1-amпјҢйӮЈйәј 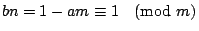 пјҢ пјҢ 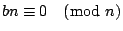 пјҢжҸӣеҸҘи©ұпјҢbn жҳҜжҲ‘еҖ‘жүҖжұӮзҡ„дёҖзө„е…¬и§ЈпјҢиӯүе®ҢгҖӮ пјҢжҸӣеҸҘи©ұпјҢbn жҳҜжҲ‘еҖ‘жүҖжұӮзҡ„дёҖзө„е…¬и§ЈпјҢиӯүе®ҢгҖӮ
зі»1пјҡе·ұзҹҘ m1 иҲҮ m2пјҢm1 иҲҮ m3пјҢвҖҰ m1 иҲҮ mt йғҪдә’иіӘпјҢйӮЈйәјдёӢеҲ—дёҖзө„еҗҢйӨҳејҸ
жңүе…¬и§ЈгҖӮ
иӯүжҳҺпјҡж №ж“ҡе·ІзҹҘжўқ件пјҢжҲ‘еҖ‘жҺЁи«– m1 иҲҮ 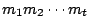 дә’иіӘгҖӮеңЁжҮүз”Ёе®ҡзҗҶ3пјҢжҲ‘еҖ‘зҹҘйҒ“ дә’иіӘгҖӮеңЁжҮүз”Ёе®ҡзҗҶ3пјҢжҲ‘еҖ‘зҹҘйҒ“
жңүе…¬и§ЈгҖӮйЎҜ然дёҠйқўйӮЈзө„еҗҢйӨҳејҸзҡ„е…¬и§Је°ұжҳҜ
зҡ„е…¬и§ЈпјҢиӯүе®ҢгҖӮ е®ҡзҗҶ4пјҡе·ұзҹҘ m1,m2,вҖҰ,mt е…©е…©дә’иіӘпјҢдёҰдё”жұӮеҮә a1 жҳҜ 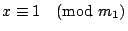 пјҢ пјҢ 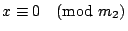 пјҢвҖҰпјҢ пјҢвҖҰпјҢ 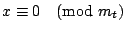 зҡ„дёҖеҖӢе…¬и§ЈпјҢa2 жҳҜ зҡ„дёҖеҖӢе…¬и§ЈпјҢa2 жҳҜ 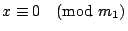 пјҢ пјҢ 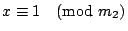 пјҢ пјҢ 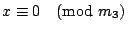 пјҢвҖҰпјҢ пјҢвҖҰпјҢ 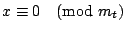 зҡ„дёҖеҖӢе…¬и§ЈпјҢд»ҘжӯӨйЎһжҺЁпјҢжұӮеҮә a3,вҖҰ,atгҖӮйӮЈ зҡ„дёҖеҖӢе…¬и§ЈпјҢд»ҘжӯӨйЎһжҺЁпјҢжұӮеҮә a3,вҖҰ,atгҖӮйӮЈ 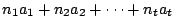 е°ұжҳҜдёӢеҲ—дёҖзө„еҗҢйӨҳејҸ е°ұжҳҜдёӢеҲ—дёҖзө„еҗҢйӨҳејҸ
зҡ„дёҖеҖӢе…¬и§ЈгҖӮ иӯүжҳҺпјҡжҲ‘еҖ‘е…ҲиӯүжҳҺ 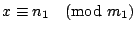 пјҢи®ҖиҖ…еҸҜд»Ҙд»ҝз…§жҲ‘еҖ‘зҡ„иӯүжі•пјҢеҺ»иӯүжҳҺе…¶йӨҳеҗҢйӨҳејҸгҖӮ ж №ж“ҡе·ұзҹҘжўқ件пјҢжҲ‘еҖ‘зҹҘйҒ“ пјҢи®ҖиҖ…еҸҜд»Ҙд»ҝз…§жҲ‘еҖ‘зҡ„иӯүжі•пјҢеҺ»иӯүжҳҺе…¶йӨҳеҗҢйӨҳејҸгҖӮ ж №ж“ҡе·ұзҹҘжўқ件пјҢжҲ‘еҖ‘зҹҘйҒ“ 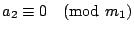 пјҢ пјҢ 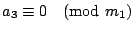 пјҢ вҖҰпјҢ пјҢ вҖҰпјҢ 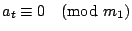 пјҢжҮүз”Ёе®ҡзҗҶ1пјҢжҲ‘еҖ‘еҫ—еҮә пјҢжҮүз”Ёе®ҡзҗҶ1пјҢжҲ‘еҖ‘еҫ—еҮә 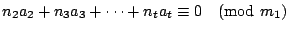 пјҢдёҰдё”е·ІзҹҘ пјҢдёҰдё”е·ІзҹҘ 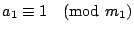 пјҢжүҖд»ҘжҮүз”Ёе®ҡзҗҶ1пјҢжҲ‘еҖ‘еҫ—еҮә пјҢжүҖд»ҘжҮүз”Ёе®ҡзҗҶ1пјҢжҲ‘еҖ‘еҫ—еҮә 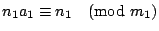 пјҢеҶҚжҮүз”ЁдёҖж¬Ўе®ҡзҗҶ1пјҢжҲ‘еҖ‘иӯүжҳҺ пјҢеҶҚжҮүз”ЁдёҖж¬Ўе®ҡзҗҶ1пјҢжҲ‘еҖ‘иӯүжҳҺ
иӯүе®ҢгҖӮ дёҠйқўзҡ„е®ҡзҗҶ4дәӢеҜҰдёҠе°ұжҳҜеӯ«еӯҗ算經裡зҡ„и§Јжі•гҖӮ a1, a2,вҖҰ,at д№ҹе°ұжҳҜеӯ«еӯҗ算經裡йқўжҸҗеҲ°зҡ„гҖҢз”Ёж•ёгҖҚгҖӮе®ҡзҗҶ4еҶҚеҠ дёҠдёӢйқўзҡ„е®ҡзҗҶ5е°ұеҗҲжҲҗдәҶж•ёи«–дёӯзҡ„еӯ«еӯҗе®ҡзҗҶгҖӮ е®ҡзҗҶ5пјҡе·ұзҹҘ m1,m2,вҖҰ,mt е…©е…©дә’иіӘгҖӮдёҰдё”жұӮеҮә a,b жҳҜдёӢеҲ—дёҖзө„еҗҢйӨҳејҸ
зҡ„е…©еҖӢе…¬и§ЈгҖӮйӮЈйәј a-b дёҖе®ҡжҳҜ 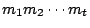 зҡ„еҖҚж•ёгҖӮеҸҚйҒҺдҫҶиӘӘпјҢ зҡ„еҖҚж•ёгҖӮеҸҚйҒҺдҫҶиӘӘпјҢ 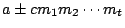 дҫӢеҰӮе®ҡзҗҶ3еҸҜд»Ҙж”№еҜ«жҲҗпјҡ е®ҡзҗҶ3пјҡе·ІзҹҘ m(x), n(x) дә’иіӘпјҢйӮЈйәјдёӢеҲ—дёҖзө„еҗҢйӨҳејҸпјҢ дҫӢеҰӮе®ҡзҗҶ3еҸҜд»Ҙж”№еҜ«жҲҗпјҡ е®ҡзҗҶ3пјҡе·ІзҹҘ m(x), n(x) дә’иіӘпјҢйӮЈйәјдёӢеҲ—дёҖзө„еҗҢйӨҳејҸпјҢ
жңүе…¬и§ЈгҖӮ еңЁиЁұеӨҡжҠҪиұЎж•ёеӯёзҡ„й ҳеҹҹдёӯпјҢд№ҹжңүеӯ«еӯҗе®ҡзҗҶгҖӮдёҚйҒҺпјҢеӣ зӮәзүҪж¶үзҡ„е…Ҙй–ҖзҹҘиӯҳеӨӘеӨҡпјҢйҖҷе…’д№ҹе°ұдёҖиЁҖиЎЁйҒҺдёҚжҸҗдәҶгҖӮ й—ңж–јеӯ«еӯҗе®ҡзҗҶпјҢзҸҫд»Јж•ёеӯёе®¶е·Іжңүе»ЈжіӣйҖҸеҫ№зҡ„з ”з©¶гҖӮи®ҖиҖ…еҰӮжһңжңүиҲҲи¶ЈпјҢеҸҜд»ҘеҸғзңӢдёҖй»һж•ёи«–еҸҠиҝ‘д»Јд»Јж•ёзҡ„жӣёзұҚгҖӮйҖҷзҜҮж·әж–Үзҡ„дё»иҰҒзӣ®зҡ„пјҢд№ҹе°ұжҳҜеј•иө·и®ҖиҖ…е°Қж•ёеӯёзҡ„иҲҲи¶ЈиҖҢе·ІгҖӮ |
|