UID98621
тИќтГљ
у▓ЙУЈ»
СИ╗жАї
уЕЇтѕє2466
уЈЙжЄЉ
уЕЇТЦхТђД
теЂТюЏ
жЂЋУдЈ
ує▒т┐Ѓ
Тјет╗БТгАТЋИ
жќ▒У«ђТгіжЎљ10
Уе╗тєіТЎѓжќЊ2008-7-29
тюеуиџТЎѓжќЊ т░ЈТЎѓ
ТюђтЙїуЎ╗жїё1970-1-1
TAуџёТ»ЈТЌЦт┐ЃТЃЁ | Тђњ
2022-6-12 03:32 PM |
|---|
у░йтѕ░тцЕТЋИ: 116 тцЕ жђБу║їу░йтѕ░: 2 тцЕ [LV.6]тИИСйЈт▒ЁТ░ЉII
|
| ТііТЋИтГИт╗║уФІТќ╝жЏєтљѕУФќСИі |
ТЋИтГИу│╗ух▒тјЪТюгжЮътИИУцЄжЏю№╝ї19СИќу┤ђуџёСИђтцДТѕљт░▒№╝їт░▒Тў»ТііжђЎтђІТЋИтГИу│╗ух▒у░Ау┤ёС║єсђѓТЋИтГИУејУФќуџёт░ЇУ▒АТюгСЙєТў»сђїТЋИсђЇтњїсђїтйбсђЇсђѓсђїтйбсђЇТў»т╣ЙСйЋтГИУејУФќуџёу»ётюЇ№╝їСйєТў»т╣ЙСйЋтЈ»С╗Цт║ДТеЎтїќ№╝їСЙІтдѓ№╝џтюет╣│жЮбт╣ЙСйЋСИГ№╝їтдѓТъюТѕЉтђЉТііС╗Ц (x,y) уѓ║т║ДТеЎуџёж╗ъуЏ┤ТјЦуюІТѕљт»дТЋИт░Ї (x,y)№╝їТѕЉтђЉСЙ┐тЈ»С╗ЦуюЂТјЅсђїтйбсђЇуџёУДђт┐х№╝їУђїуЏ┤ТјЦС╗Цт»дТЋИСЙєУејУФќт«ЃС║єсђѓУЄ│Тќ╝т»дТЋИ№╝їDedekind тњї Cantor тюе19СИќу┤ђСИГУЉЅтљёт╝ЋтЁЦСИђтЦЌт»дТЋИуџёуљєУФќ№╝їС╗ЦТюЅуљєТЋИуѓ║у┤аТЮљТііт»дТЋИт╗║ТДІтЄ║СЙє№╝їТюЅуљєТЋИ 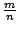 тЈ»С╗ЦТЃ│ТѕљТЋ┤ТЋИт░Ї (m,n)№╝їтЁХСИГ тЈ»С╗ЦТЃ│ТѕљТЋ┤ТЋИт░Ї (m,n)№╝їтЁХСИГ 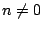 №╝ЏУІЦ (m',n') уѓ║тЈдСИђтђІжђЎуе«ТЋ┤ТЋИт░Ї№╝їтЅЄуЋХ mn'=m'n ТЎѓ№╝їТѕЉтђЉТіі №╝ЏУІЦ (m',n') уѓ║тЈдСИђтђІжђЎуе«ТЋ┤ТЋИт░Ї№╝їтЅЄуЋХ mn'=m'n ТЎѓ№╝їТѕЉтђЉТіі 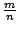 тњї тњї 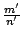 уюІТѕљуГЅтљї№╝їжђЎТеБТѕЉтђЉСЙ┐тЈ»С╗ЦућеТЋ┤ТЋИуѓ║у┤аТЮљТііТюЅуљєТЋИт╗║ТДІтЄ║СЙєС║є№╝їУЄ│Тќ╝ТЋ┤ТЋИ№╝їС╣ЪтЈ»С╗ЦућежАъС╝╝уџёТќ╣Т│ЋтЙъТГБТЋ┤ТЋИт╗║ТДІтЄ║СЙєсђѓтдѓТГцТѕЉтђЉтЈ»С╗ЦТііТЋ┤тђІТЋИтГИт╗║уФІтюеТГБТЋ┤ТЋИСИісђѓ тюе19СИќу┤ђСИГУЉЅ№╝їCantor тЅхуФІС║єжЏєтљѕУФќсђѓТа╣ТЊџС╗ќуџёУффТ│Ћ№╝їуЋХТѕЉтђЉТііСИђС║ЏТИЁТЎ░тЈ»тѕєуџё№╝їт«бУДђСИќуЋїСИГТѕќТѕЉтђЉТђЮТЃ│СИГуџёС║ІуЅЕ№╝їуюІТѕљСИђжФћТЎѓ№╝їжђЎТЋ┤жФћСЙ┐уе▒С╣Іуѓ║сђїжЏєтљѕсђЇ№╝їтЁХСИГуџёС║ІуЅЕуе▒уѓ║т«ЃуџёсђїтЁЃу┤асђЇсђѓУІЦ x Тў»жЏєтљѕ A уџётЁЃу┤а№╝їТѕЉтђЉСЙ┐ућеугдУЎЪ уюІТѕљуГЅтљї№╝їжђЎТеБТѕЉтђЉСЙ┐тЈ»С╗ЦућеТЋ┤ТЋИуѓ║у┤аТЮљТііТюЅуљєТЋИт╗║ТДІтЄ║СЙєС║є№╝їУЄ│Тќ╝ТЋ┤ТЋИ№╝їС╣ЪтЈ»С╗ЦућежАъС╝╝уџёТќ╣Т│ЋтЙъТГБТЋ┤ТЋИт╗║ТДІтЄ║СЙєсђѓтдѓТГцТѕЉтђЉтЈ»С╗ЦТііТЋ┤тђІТЋИтГИт╗║уФІтюеТГБТЋ┤ТЋИСИісђѓ тюе19СИќу┤ђСИГУЉЅ№╝їCantor тЅхуФІС║єжЏєтљѕУФќсђѓТа╣ТЊџС╗ќуџёУффТ│Ћ№╝їуЋХТѕЉтђЉТііСИђС║ЏТИЁТЎ░тЈ»тѕєуџё№╝їт«бУДђСИќуЋїСИГТѕќТѕЉтђЉТђЮТЃ│СИГуџёС║ІуЅЕ№╝їуюІТѕљСИђжФћТЎѓ№╝їжђЎТЋ┤жФћСЙ┐уе▒С╣Іуѓ║сђїжЏєтљѕсђЇ№╝їтЁХСИГуџёС║ІуЅЕуе▒уѓ║т«ЃуџёсђїтЁЃу┤асђЇсђѓУІЦ x Тў»жЏєтљѕ A уџётЁЃу┤а№╝їТѕЉтђЉСЙ┐ућеугдУЎЪ 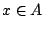 УАеуц║№╝ЏУІЦ x СИЇТў»жЏєтљѕ A уџётЁЃу┤асђѓтЅЄС╗Ц УАеуц║№╝ЏУІЦ x СИЇТў»жЏєтљѕ A уџётЁЃу┤асђѓтЅЄС╗Ц 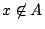 УАеуц║№╝ЏУђїСИЇтїЁтљФС╗╗СйЋтЁЃу┤ауџёжЏєтљѕтЈФсђїуЕ║жЏєтљѕсђЇсђѓжђџтИИућеугдУЎЪ УАеуц║№╝ЏУђїСИЇтїЁтљФС╗╗СйЋтЁЃу┤ауџёжЏєтљѕтЈФсђїуЕ║жЏєтљѕсђЇсђѓжђџтИИућеугдУЎЪ 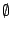 УАеуц║т«Ѓ№╝їуЕ║жЏєтљѕтњїТЋИу│╗СИГуџё 0 уЏИуЋХсђѓућ▒тЁЃу┤а a,b,c уѓ║тЁЃу┤ауџёжЏєтљѕ№╝їтЈ»С╗ЦућеугдУЎЪ {a,b,c} УАеуц║сђѓТюЅС║єжђЎС║ЏТ║ќтѓЎС╗ЦтЙї№╝їТѕЉтђЉт░▒тЈ»С╗ЦТііТГБТЋ┤ТЋИуџёу│╗ух▒т╗║уФІтюежЏєтљѕУФќСИі№╝їТќ╣Т│ЋТў»№╝џ УАеуц║т«Ѓ№╝їуЕ║жЏєтљѕтњїТЋИу│╗СИГуџё 0 уЏИуЋХсђѓућ▒тЁЃу┤а a,b,c уѓ║тЁЃу┤ауџёжЏєтљѕ№╝їтЈ»С╗ЦућеугдУЎЪ {a,b,c} УАеуц║сђѓТюЅС║єжђЎС║ЏТ║ќтѓЎС╗ЦтЙї№╝їТѕЉтђЉт░▒тЈ»С╗ЦТііТГБТЋ┤ТЋИуџёу│╗ух▒т╗║уФІтюежЏєтљѕУФќСИі№╝їТќ╣Т│ЋТў»№╝џ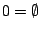 , 1={0}, 2={0,1}, 3={0,1,2}№╝їтдѓТГцТЋ┤тђІТЋИтГИСЙ┐тЈ»С╗Цт╗║уФІтюежЏєтљѕУФќСИіС║єсђѓ , 1={0}, 2={0,1}, 3={0,1,2}№╝їтдѓТГцТЋ┤тђІТЋИтГИСЙ┐тЈ»С╗Цт╗║уФІтюежЏєтљѕУФќСИіС║єсђѓ |
|